The MLP Distribution Function
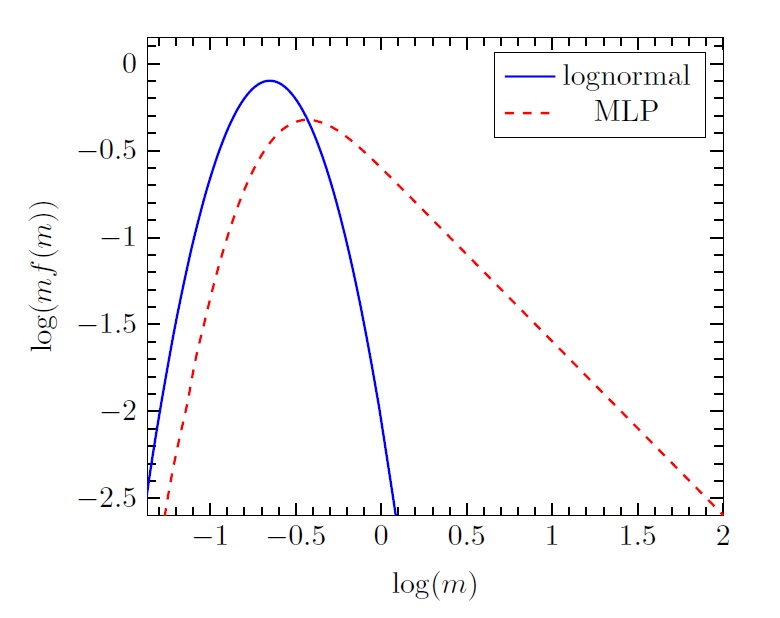There are many disciplines in which a desired distribution is one that is like a lognormal at low and intermediate values, with a characteristic peak and turnover, but transitions to a power law distribution at high values. Besides astronomy, this need has arisen in fields as diverse as biology, computer science, ecology, and finance, to name several. A review of common statistical resources reveals that very few analytic functions of this type exist, hence the attempts to fit empirical distributions by patching together different functions over different domains. Power-law distributions were first introduced by Pareto to explain the distribution of incomes seen in data from many different countries. The distribution of city sizes also shows a power-law character and regularity across many countries. It is referred to as Zipf's Law.
In recent papers, we have analyzed and characterized the properties of a hybrid three-parameter probability density function (pdf) (Basu, Gil, and Auddy 2015; see also Basu and Jones 2004) that can be used to fruitfully model data sets that exhibit both lognormal-like and power-law behavior. Indeed, this modified lognormal power-law (MLP) distribution
has the advantage that it introduces only one additional parameter beyond that in the lognormal. As a result, it is a natural first step when fitting data that may look like a modified lognormal, and its relatively compact analytic closed-form expression makes it easy to use with common fitting techniques.
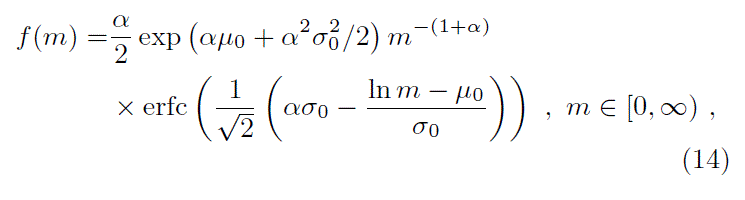
An IDL routine for drawing random samples from the MLP distribution