Star Formation from the Fragmentation of Interstellar Molecular Clouds
Ever since Isaac Newton wrote down the law of gravity, scientists (starting with Newton himself) have known that a large gravitating mass may be prone to fragment into a large number of individually collapsing fragments, that then go on to form stars. In recent years, astronomers have realized that the process of gravitational fragmentation is strongly regulated by magnetic forces (as well as magnetic field dissipation - by ambipolar diffusion in the fragmentation stage) and turbulent motions (as well as turbulent dissipation). Work in our group is one of the few in the world that has solved the equations of non-ideal magnetohydrodynamics to calculate the evolution of such processes as they affect gravitational fragmentation. This is interesting because magnetic fields can explain the observed very low efficiency of formation of molecular gas into stars. Only a few percent of molecular cloud mass is converted into stars in typical observed star-forming regions. We have published a comprehensive set of papers on the early stages of star formation, as regulated by these processes. A linear analysis of instability in thin layers ( Ciolek & Basu 2006) yielded the result that the preferred fragmentation scale is a sensitive function of the ambient mass-to-flux ratio, as is the time scale for instability. Numerical simulations of the nonlinear evolution (Basu & Ciolek 2004; Basu et al. 2009a; Basu et al. 2009b) yields definitive quantitative predictions for sizes, shapes, and masses of star-forming "cores", as well as infall speeds and overall morphology of clouds. Moreover, these properties are sensitive functions of the ambient magnetic field strength. The addition of highly turbulent initial conditions leads to yet another set of distinct outcomes. For example, infall speeds at core boundaries are highly supersonic in such cases, but only subsonic in the magnetically-dominated models. These are testable differences.
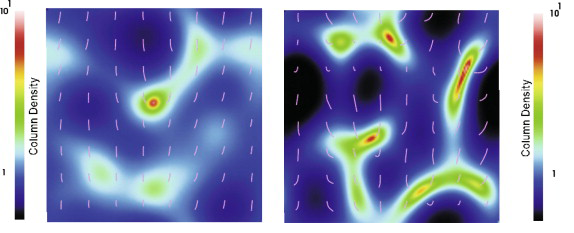 Fig. 1 shows the difference in column density and magnetic field morphology by the time of runaway collapse, for either transcritical (left; dimensionless mass-to-flux ratio &mu0 = 1.0, i.e. the critical value for collapse) or supercritical (right; &mu0 = 2.0) clouds. Both models start out with small-amplitude initial perturbations. We propose that magnetic field curvature, as traced by polarization of dust emission, can measure a cloud's ambient mass-to-flux ratio (Basu et al. 2009a). The above work is done in the limit that the self-gravitating layer is geometrically thin and can be treated as a sheet in many respects. Fully three-dimensional non-ideal magnetohydrodynamic simulations ( Kudoh, Basu, Ogata, and Yabe 2007; Kudoh and Basu 2008) have verified that the main results presented above are generic to the fragmentation process.
Fig. 1 shows the difference in column density and magnetic field morphology by the time of runaway collapse, for either transcritical (left; dimensionless mass-to-flux ratio &mu0 = 1.0, i.e. the critical value for collapse) or supercritical (right; &mu0 = 2.0) clouds. Both models start out with small-amplitude initial perturbations. We propose that magnetic field curvature, as traced by polarization of dust emission, can measure a cloud's ambient mass-to-flux ratio (Basu et al. 2009a). The above work is done in the limit that the self-gravitating layer is geometrically thin and can be treated as a sheet in many respects. Fully three-dimensional non-ideal magnetohydrodynamic simulations ( Kudoh, Basu, Ogata, and Yabe 2007; Kudoh and Basu 2008) have verified that the main results presented above are generic to the fragmentation process.