Radial Velocities
The term 'radial velocity' means the component of velocity along the line of sight to the object. The Doppler shift in the light is used to measure the radial velocity using the standard formula v = Dm c/m, where m is the wavelength of light, c is the velocity of light (2.99792458 x 105 km/s), and Dm is the wavelength shift. We exploit the sharpness of spectral lines to measure the shifts. The sharper the lines, the better the determination.
In order to measure the wavelength shift, we need to know the intrinsic wavelength of the line or lines. This is usually measured in a laboratory setting by specialists. Second, we need to know the observed wavelength on an absolute scale. Observed wavelengths are calibrated using reference lamps, or telluric lines, or laser standards.
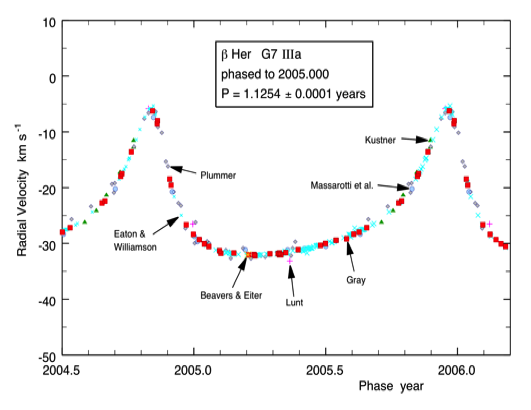
Radial velocities are used to measure motions of stars in space, binary star or extra-solar planet orbits, pulsating stars, and chaotic motions in stellar photospheres. Here is an example of radial velocities showing the orbital motion of Beta Her. See also the third signature of stellar granulation.
Radial velocity variation of the binary star b Her; from 2016 ApJ 832, 68.
For stars on the cool half of the HR diagram, those with convective envelopes, the granulation in the photosphere will induce a small blueshit of less than ~ 1 km/s. The third signature of granulation can be used to correct for this effect. See 2009 ApJ 697, 1032 for details. One should also bear in mind the presence of the gravitational redshift given by GM/(Rc2), where G is the gravitational constant, M is the mass, R the radius, and c the velocity of light. For the Sun, it has a value of 636 m/s. For the Earth it has a value of 3 m/s. Therefore the solar value seen from Earth is 633 m/s.