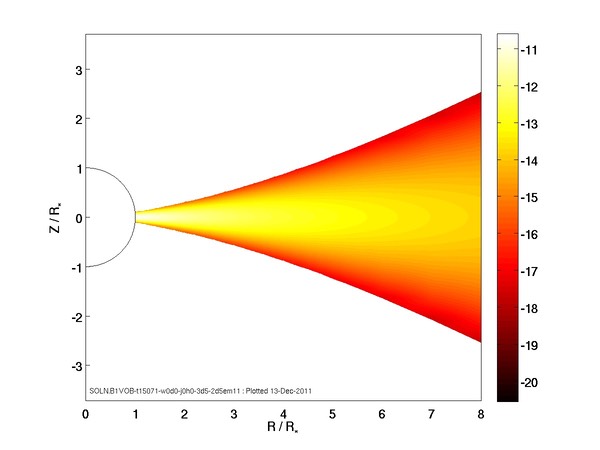
An important property of a circumstellar disk is how the gas density varies from point to point in the disk. Ultimately one would hope to predict this from the basic physical mechanism that ejects the gas into the disk from. However, the physical mechanism is unknown for the Be stars. For this reason, simple density models that contain adjustable parameters are often used. The image above shows one such model. Here the density of the disk gas (in g/cm3) is shown as a function of distance from the star (R/R*) and height above and below the plane of the disk (+/- Z/R*). The star is shown as a circular outline. In the colour bar to the right, dense gas is shown as nearly white, while rarified gas is dark red. The disk density is is assumed to drop as a power-law with distance from the star and exponentially above and below the plane of the disk. Note that the latter assumption means that the disk is actually quite thin compared to the radius of the star, something that is not well represented by the image above. Looking at the colour bar, you can determine from the image colours that the density contrast from the plane of the disk (Z/R*=0) to the upper edge is more than a factor of one million! The total mass of the disk follows directly from the density and in the case of Be stars, the disks are thought to be of negligible mass compared to the central B star, typically from one hundred millionth to a billionth of the star's mass. The density structure has a strong impact in determining what we will "see" from the disk. But before such predictions can be made, one other critical disk variable must be computed: how the gas temperature varies from point to point in the disk.