

Nuclear reactions and nuclear fission
- The general theory of reactions between nuclei is too advanced
for this course. Again we will resort to simple models that provide
insight. In the case of a reaction between a bombarding particle and a
target nucleus, we could imagine two rather different (idealized) ways
in which reactions could occur. For definiteness, consider the
following reaction:
At one extreme, the reaction could proceed via a compound
nucleus - the deuteron could be absorbed by the potassium, yielding
a 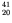 Ca
Ca nucleus in an excited state, which rattles
around until it forgets about its origin and finally emits a
proton. Alternatively, the reaction could occur directly - upon
hitting the surface of the potassium, the neutron could become detached
from the proton (the binding energy is only 2.2 MeV) and be absorbed
by the nucleus, while the proton continues on its way (a stripping
process); or the deuteron could be absorbed at the surface of the
potassium, ejecting a proton as it enters (a knockout reaction). These
different modes of reaction, which all end up with a proton leaving
the potassium nucleus, may be distinguished by the rather different
angular distributions of the ejected proton that are predicted.
nucleus in an excited state, which rattles
around until it forgets about its origin and finally emits a
proton. Alternatively, the reaction could occur directly - upon
hitting the surface of the potassium, the neutron could become detached
from the proton (the binding energy is only 2.2 MeV) and be absorbed
by the nucleus, while the proton continues on its way (a stripping
process); or the deuteron could be absorbed at the surface of the
potassium, ejecting a proton as it enters (a knockout reaction). These
different modes of reaction, which all end up with a proton leaving
the potassium nucleus, may be distinguished by the rather different
angular distributions of the ejected proton that are predicted.
- We have already seen that when a nucleus is bombarded by
particles (e.g. neutrons, protons), the number of particles
interacting with the nucleus or scattered out of the beam varies
rapidly with energy, with local peaks in the number of particles
scattered at specific energies associated with energy levels of the
target nucleus. This is an example of resonance scattering. We
may analyze this reaction using the compound nucleus model.
- It is found that resonance scattering occurs when the
bombarding particle is captured by the nucleus, a process which is
particularly likely to occur when the incoming particle carries just
the right amount of kinetic energy to bring the nucleus to one of its
excited states. This forms an excited compound nucleus state, which
then after a while decays. Such an experiment is particularly easy to
analyze when the incoming particle re-emerges (this is only one of the
possible final states).
- We have seen earlier that the lifetime of a state
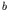 is
is
where 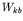 is the transition rate (probability per second)
for transitions from
is the transition rate (probability per second)
for transitions from 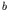 to
to 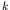 , and
, and 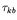 is lifetime
for decay to a specific state
is lifetime
for decay to a specific state 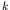 . We also define partial and total
widths
. We also define partial and total
widths
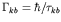 and
and
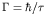 ; the gammas have units of energy.
; the gammas have units of energy.
- We now consider a system initially in the form of a bombarding
particle (e.g. a neutron) and a target nucleus
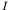 . The system forms a
excited state of the compound nucleus
. The system forms a
excited state of the compound nucleus 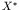 and then decays to a two
particle final state again. We will essentially consider these two
steps separately, ignoring the effects of spin.
and then decays to a two
particle final state again. We will essentially consider these two
steps separately, ignoring the effects of spin.
- Initially, the system is in a state
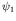 , which is one of a
complete orthonormal set of (approximately stationary) states of the
system,
, which is one of a
complete orthonormal set of (approximately stationary) states of the
system, 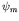 . We have seen earlier (Lecture 2, p 5) that we may
write the exact state of the system as a superposition of these
stationary states
. We have seen earlier (Lecture 2, p 5) that we may
write the exact state of the system as a superposition of these
stationary states
where 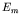 is the energy of state
is the energy of state 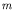 . We found that this leads to
. We found that this leads to
- Now we suppose that the system is initially in state
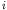 so
so
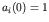 and all other
and all other 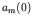 's are zero. We are interested in
the case in which the system forms the specific compound nucleus
system
's are zero. We are interested in
the case in which the system forms the specific compound nucleus
system 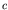 . For times not too long after
. For times not too long after 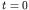 when the incoming
neutron approaches the target, the probability amplitude (while
when the incoming
neutron approaches the target, the probability amplitude (while
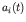 is still nearly 1) of finding the system in
is still nearly 1) of finding the system in 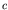 satisfies
approximately
satisfies
approximately
Here the first term describes the probability of making the transition
into state 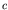 and the second lumps together all the ways of leaving
and the second lumps together all the ways of leaving
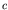 that lead to the mean lifetime
that lead to the mean lifetime 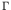 of this state.
of this state.
- This equation may be rewritten as
Integrating from 0 to
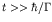 and dividing by
and dividing by
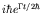 , we find the probability that the system is in
state
, we find the probability that the system is in
state 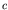 to be
to be
and recalling that the decay rate of 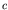 into the final state (channel
into the final state (channel
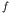 ) is
) is
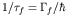 , the decay rate to
, the decay rate to 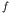 may be
written as
may be
written as
- Now the incoming particle is described by a wave function
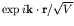 in the centre of mass coordinate
system, and
in the centre of mass coordinate
system, and 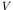 is the (artificial) volume of the box the system is
in. The particle flux is given by the particle density times the
beam velocity,
is the (artificial) volume of the box the system is
in. The particle flux is given by the particle density times the
beam velocity, 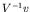 , and so the cross section for transitions
from channel
, and so the cross section for transitions
from channel 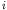 to channel
to channel 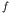 is given by
is given by
- From Fermi's golden rule (Lecture 2, p 7), the width of
the decay from state
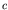 to the initial state
to the initial state 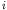 which has
energy
which has
energy 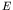 is
is
where 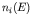 is the density of states around
is the density of states around 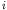 , which we
have seen is
, which we
have seen is
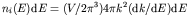 . Since
. Since
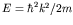 ,
,
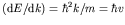 .
.
- Finally putting everything together, we get
so
This important result is often called the Breit-Wigner formula.
- Points to notice:
- The cross section
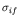 is peaked around
is peaked around 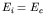 and falls to half its peak value at
and falls to half its peak value at 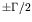 (hence the
term ``width'' for
(hence the
term ``width'' for 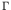 ).
).
- The width of the resonant peak depends on the lifetime of the
compound nucleus intermediate state; measurement of the width provides
an estimate of this lifetime.
- The derivation ignores the contribution of non-resonant
scattering, which contributes a cross section of about the geometrical
value,
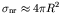 far from resonances.
far from resonances.
- This expression predicts that the maximum cross section can be
of order
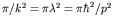 , where
, where
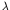 is the de Broglie wavelength of the incoming neutron. For
low energy bombarding particles, this can be quite a lot larger than
the (non-resonant) geometrical cross section.
is the de Broglie wavelength of the incoming neutron. For
low energy bombarding particles, this can be quite a lot larger than
the (non-resonant) geometrical cross section.
- The non-resonant scattering term interferes with the resonant
one, so that the cross section drops below the geometrical value on
one side of a resonance.
- The cross section for interaction of a neutron beam with a
target does not fall off rapidly with energy because there is no
Coulomb barrier to surmount. Neutrons can be absorbed by a nucleus
even at
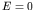 . At sufficiently low energies,
. At sufficiently low energies, 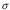 usually rises as
usually rises as
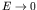 , so that the cross section follows a
``
, so that the cross section follows a
``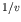 '' law.
'' law.
- This can be made plausible for the case where the low energy
limit is not too far from a resonance, so that we may use the
Breit-Wigner formula. Recall from Fermi's golden rule that
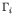 is proportional to the density of states times a matrix element. If we
suppose that the matrix element does not change much at low energy,
then
is proportional to the density of states times a matrix element. If we
suppose that the matrix element does not change much at low energy,
then 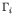 depends on energy as
depends on energy as
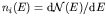 which is proportional to
which is proportional to 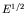 or
or 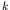 . Taking this dependence
into account, the variation of
. Taking this dependence
into account, the variation of 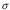 for neutron interaction goes
as
for neutron interaction goes
as
which varies as 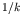 or
or 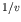 as
as
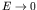 .
.
- For reactions of charged particles with other nuclei, one must
take the Coulomb repulsion into account. We may get an idea of how
this changes things by looking at the specific case of bombardment of
a target by alpha particles. We use the Breit-Wigner formula, which may be
written as
by recalling that
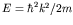 . Now we have seen in the case of
alpha decay that the probability per second of decay for
energies small compared to the Coulomb barrier is
. Now we have seen in the case of
alpha decay that the probability per second of decay for
energies small compared to the Coulomb barrier is
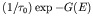 . This is also equal to
. This is also equal to
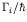 , and
making this substitution and letting
, and
making this substitution and letting 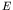 become much smaller than the
energy
become much smaller than the
energy 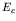 of the lowest resonance, we find
of the lowest resonance, we find
This shows that the cross section for interaction goes to 0
exponentially as
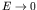 .
.
- This result is an example of more general behaviour of the
interaction cross section for charged particles. We see that our
result may be written as
where 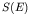 is approximately constant for small enough
is approximately constant for small enough 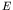 . This
behaviour is quite general, and it is common to describe low-energy
experimental data by specifying
. This
behaviour is quite general, and it is common to describe low-energy
experimental data by specifying 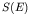 . This is particularly useful in
stellar astrophysics which often needs reaction cross sections at
lower energies than those at which they can be measured.
. This is particularly useful in
stellar astrophysics which often needs reaction cross sections at
lower energies than those at which they can be measured.
- One extremely important aspect of nuclear physics is its
application as a source of energy for society. At present about 1/6th
of world energy generation comes from nuclear power. In Ontario,
almost half the electric power generation comes from nuclear power
plants.
- One expects that fission of very heavy elements could provide a
good energy source because of the decline of the average binding
energy per nucleon beyond iron from a peak of somewhat more than 8.5
MeV per nucleon to about 7.5 MeV per nucleon. This means that if a
nucleus with
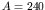 fissions, about 1 MeV per nucleon will be
released, providing in total roughly 200 MeV per fission. Thus
fissioning 1 kg of U should release about
fissions, about 1 MeV per nucleon will be
released, providing in total roughly 200 MeV per fission. Thus
fissioning 1 kg of U should release about
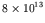 J (about
20 million kWh), compared to the energy release by burning (oxidizing)
1 kg of natural gas which releases roughly
J (about
20 million kWh), compared to the energy release by burning (oxidizing)
1 kg of natural gas which releases roughly 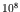 J or about 2 kWh.
J or about 2 kWh.
- The most suitable naturally occurring fuel is uranium, which is
available in adequate deposits for mining in regions of old
continental shield such as northern Canada. It occurs primarily in two
forms,
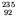 U (0.7%) and
U (0.7%) and
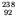 U
(99.3%). For uranium ore, the natural rate of fission is completely
negligible, but U may be made to fission by neutron capture, and as
each fission results in neutron-rich daughter nuclei which release a
couple of neutrons that may in turn be captured, the possibility of a
self-sustaining reaction exists.
U
(99.3%). For uranium ore, the natural rate of fission is completely
negligible, but U may be made to fission by neutron capture, and as
each fission results in neutron-rich daughter nuclei which release a
couple of neutrons that may in turn be captured, the possibility of a
self-sustaining reaction exists.
- When a uranium nucleus captures a neutron, the nucleon enters
the nucleus in an excited state of energy equal to the binding energy
of the last neutron plus the (centre-of-mass) kinetic energy of the
neutron at the instant of capture. If this excitation energy is larger
than the Coulomb barrier height of 5 to 6 MeV, the nucleus will
fission immediately; otherwise it may well de-excite radiatively
without fissioning. Here there is an important difference between the
two natural isotopes of uranium;
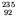 U changes from an
odd-even to an even-even nucleus on neutron capture, while
U changes from an
odd-even to an even-even nucleus on neutron capture, while
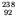 U makes the opposite change. Because of the
symmetry energy term in the semi-empirical binding energy formula,
the new neutron has higher excitation energy in
U makes the opposite change. Because of the
symmetry energy term in the semi-empirical binding energy formula,
the new neutron has higher excitation energy in
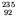 U
(about 6.46 MeV even without any kinetic energy) than in
U
(about 6.46 MeV even without any kinetic energy) than in
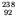 U (only 4.78 MeV plus kinetic energy). This difference is just
large enough that
U (only 4.78 MeV plus kinetic energy). This difference is just
large enough that
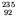 U fissions even on capture of a
thermal neutron, but
U fissions even on capture of a
thermal neutron, but
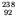 U must capture a neutron having
at least 1.4 MeV of energy to fission.
U must capture a neutron having
at least 1.4 MeV of energy to fission.
- Another important difference between the two natural isotopes of
uranium is that - apart from resonances - the interaction cross
section for fission is roughly constant around 10 barns from thermal
energies to several MeV for
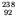 U, while the fission
cross section of
U, while the fission
cross section of
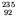 U is more than 100 barn and rising
below about 1 eV. Thus thermal neutrons are more easily captured in
U is more than 100 barn and rising
below about 1 eV. Thus thermal neutrons are more easily captured in
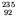 U, by a factor large enough to almost make up for
the low abundance of this isotope.
U, by a factor large enough to almost make up for
the low abundance of this isotope.
- On fission, the two highly excited fission fragments very
quickly boil off on average about
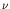 = 2.5 neutrons, plus about
= 2.5 neutrons, plus about
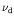 = 0.02 more
after some beta-decays and a delay of some seconds. The total energy
release, mostly in the form of the kinetic energy of the fission
fragments, is about 205 MeV. (Some 12 MeV escapes with neutrinos from
the beta decays.)
= 0.02 more
after some beta-decays and a delay of some seconds. The total energy
release, mostly in the form of the kinetic energy of the fission
fragments, is about 205 MeV. (Some 12 MeV escapes with neutrinos from
the beta decays.)
- The results of fission followed by release of neutrons which
cause other fissions depends sensitively on the number of neutrons
released and captured per fission. If
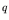 is th probability of
capture, then the change in the number
is th probability of
capture, then the change in the number 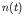 of free neutrons in d
of free neutrons in d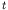 is
is
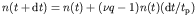 where
where 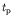 is the time-scale for a neutron to either react or
somehow escape from the system. This equation leads to
is the time-scale for a neutron to either react or
somehow escape from the system. This equation leads to
with solution
Thus the number of reaction either falls off rapidly or increases
catastrophically depending on whether 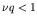 (uranium ore
situation) or
(uranium ore
situation) or 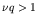 (nuclear bomb). Only for
(nuclear bomb). Only for 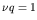 - the
reaction rate balanced on a knife-edge - can we get useful power
generation.
- the
reaction rate balanced on a knife-edge - can we get useful power
generation.
- A typical fission neutron has an energy of about 2 MeV. The
total cross section for such neutrons is about 7 barns, so the mean
free path
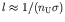 where
where 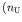 is the
number density of uranium atoms in the pure metal, about
is the
number density of uranium atoms in the pure metal, about
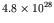 nuclei per cubic meter. The mean free path is thus about 3
cm. For pure
nuclei per cubic meter. The mean free path is thus about 3
cm. For pure
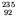 U, the scattering cross section is
about 5 times larger than the cross section for fission, so the
neutron typically goes several cm before causing another fission,
requiring about
U, the scattering cross section is
about 5 times larger than the cross section for fission, so the
neutron typically goes several cm before causing another fission,
requiring about
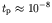 s for this. Thus if the
reaction is exponentially increasing, the time-scale for explosion is
less than 1 microsecond once a critical mass (about 50 kg of
s for this. Thus if the
reaction is exponentially increasing, the time-scale for explosion is
less than 1 microsecond once a critical mass (about 50 kg of
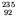 U, or a sphere of about 17 cm diameter) has been
assembled.
U, or a sphere of about 17 cm diameter) has been
assembled.
- Now consider the possibility of a power reactor. With natural
uranium fuel, a 2 MeV neutron can cause fission in either isotope, but
the probability of scattering (inelastically) is about 20 times higher
than that of causing fission in
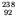 U, so the neutron
quickly drops in energy below the fission threshold. Thus
U, so the neutron
quickly drops in energy below the fission threshold. Thus
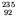 U is not directly usable as a fuel. Now as the neutron energy
drops, it has a fair probability of being absorbed by
U is not directly usable as a fuel. Now as the neutron energy
drops, it has a fair probability of being absorbed by
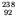 U without causing fission. (This produces the useful fuel - and
bomb-making material - plutonium
U without causing fission. (This produces the useful fuel - and
bomb-making material - plutonium
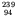 Pu after two beta
decays, thus leading to the possibility of a breeder reactor, a
nuclear reactor that creates more fuel than it uses.)
Pu after two beta
decays, thus leading to the possibility of a breeder reactor, a
nuclear reactor that creates more fuel than it uses.)
- In the usual thermal reactor, the drop in energy is deliberately
controlled in such a way as to lead to fission of the
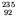 U fuel in the reactor and also to control the power output. The
fuel is in the form of thin rods embedded in a substance (the moderator) of low mass number and low neutron absorption cross
section. The neutrons quickly escape from the fuel rod (leading to low
probability of capture by
U fuel in the reactor and also to control the power output. The
fuel is in the form of thin rods embedded in a substance (the moderator) of low mass number and low neutron absorption cross
section. The neutrons quickly escape from the fuel rod (leading to low
probability of capture by
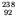 U) and lose their energy
by elastic collisions with the moderator until most have reached the
thermal energy of the reactor, about 0.1 eV. Because of the large
capture cross section for such neutrons by
U) and lose their energy
by elastic collisions with the moderator until most have reached the
thermal energy of the reactor, about 0.1 eV. Because of the large
capture cross section for such neutrons by
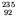 U, enough
neutrons are captured to make the reaction self-sustaining. The
moderator is usually carbon or heavy water D
U, enough
neutrons are captured to make the reaction self-sustaining. The
moderator is usually carbon or heavy water D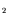 O (the high neutron
capture cross section of normal H makes ordinary water unsuitable for
a natural fuel reactor). Control is achieved by inserting boron or
cadmium rods into the reactor core; the large capture cross section of
B or Cd for neutrons leads to a decrease in the neutron flux and slows
the reactor down.
O (the high neutron
capture cross section of normal H makes ordinary water unsuitable for
a natural fuel reactor). Control is achieved by inserting boron or
cadmium rods into the reactor core; the large capture cross section of
B or Cd for neutrons leads to a decrease in the neutron flux and slows
the reactor down.
Nuclear reactions and nuclear fission
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html lec9-nucl_reacts.tex
The translation was initiated by on 2002-03-18


2002-03-18